Visualising Athlete Change Scores

Example 1

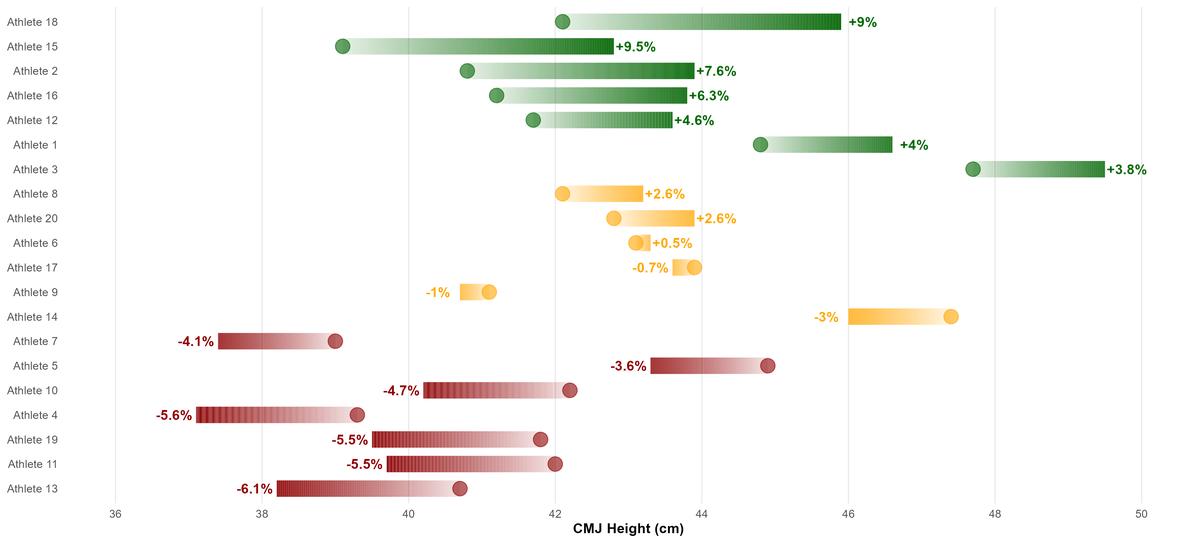
Dumbbell plots are a neat way to visualise change between two data points, such as between test-retest CMJ scores, and this can easily be done with geom_dumbbell() from the ggalt package. However, I’m creating a kind of custom dummbbell plot by adopting an approach I’ve used previously for some of my other analytics work. This requires the ggforce package which I’m simply using as I prefer the way the colours are visualised. Here’s the code.

library(ggforce)

ggplot(dat) +
  geom_link(aes(x = best, xend = retest, y = athlete, yend = athlete,
                colour = colour, alpha = stat(index)),
            show.legend = FALSE, size = 6, n = 500) +
  scale_colour_identity() +
  geom_point(aes(x = best, y = athlete, colour = colour), shape = 19,
             size = 5, alpha = 0.6) +
  scale_x_continuous(limits = c(36, 50),
                     breaks = scales::pretty_breaks(n = 8)) +
  theme_minimal() +
  labs(x = "CMJ Height (cm)") +
  theme(panel.grid.minor.x = element_blank(),
        panel.grid.major.y = element_blank(),
        axis.title.x = element_text(face = "bold"),
        axis.title.y = element_blank()) +
  ### LABELS ###
  geom_text(data = subset(dat, pct_change < cv * -1),
            aes(x = retest, y = athlete, fontface = "bold",
                label = paste0(pct_change, "%")), color = "darkred",
                nudge_x = -0.3) +
  geom_text(data = subset(dat, pct_change > cv),
            aes(x = retest, y = athlete, fontface = "bold",
                label = paste0("+", pct_change, "%")), color = "darkgreen",
            nudge_x = 0.3) +
  geom_text(data = subset(dat, pct_change < 0 & pct_change >= cv * -1),
            aes(x = retest, y = athlete, fontface = "bold",
                label = paste0(round(pct_change, 1), "%")), color = "orange",
            nudge_x = -0.3) +
  geom_text(data = subset(dat, pct_change > 0 & pct_change <= cv),
            aes(x = retest, y = athlete, fontface = "bold",
                label = paste0("+", round(pct_change, 1), "%")),
            color = "orange", nudge_x = 0.3)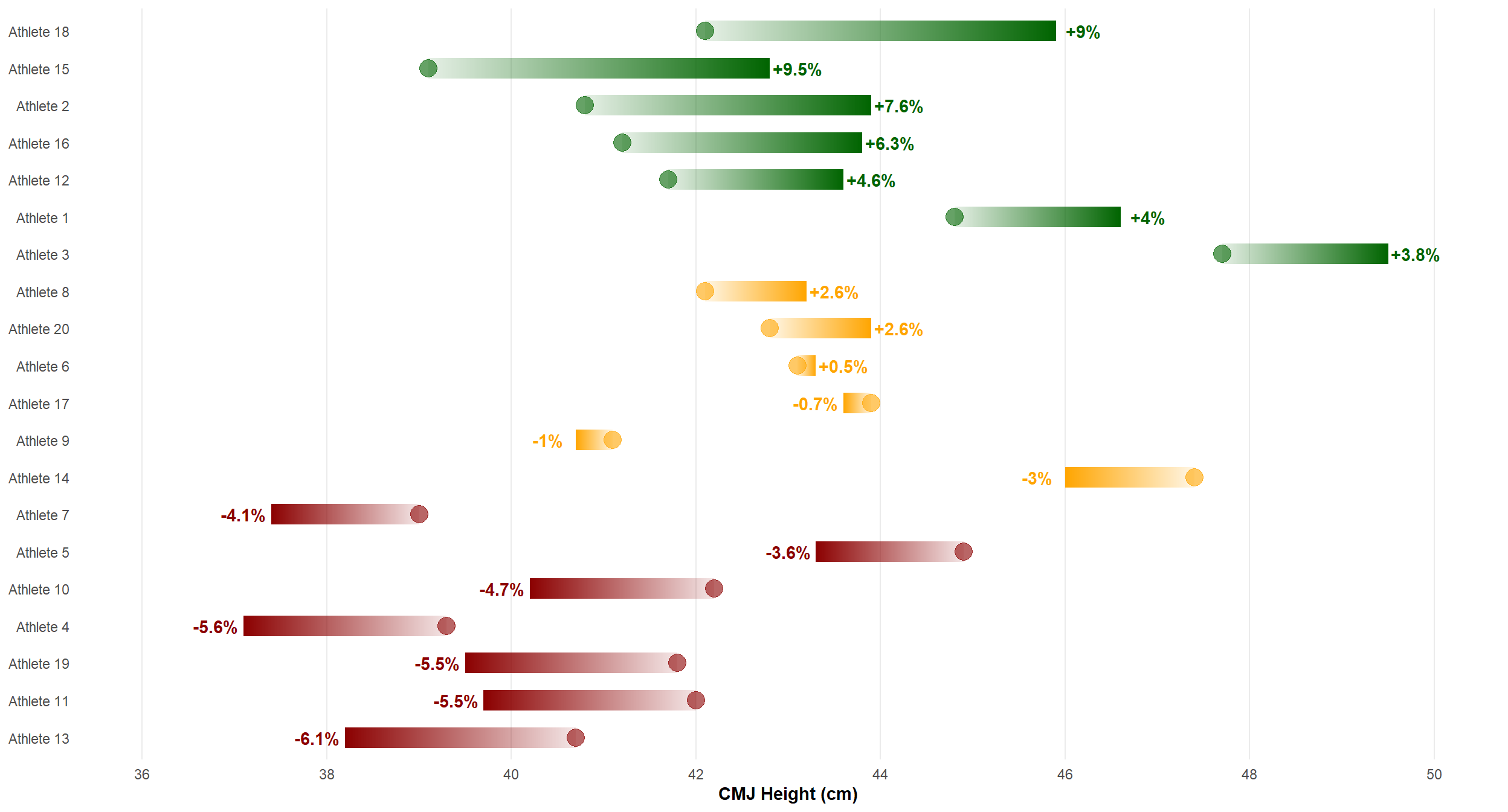

geom_link() connects two data points much like the way geom_dumbbell() does. The points represent each athlete’s baseline CMJ result - their best from the reliability trials - while the end of the link is their retest score. The sequential progression of the colours in the direction of the link (best → retest) is something I personally really like here. The links are based on the raw CMJ values, but I’m reporting the labels in geom_text() as a percentage change.

Example 2

We could also use a similar approach to plot the percentage change (pct_change) from best to retest relative to 0.

ggplot(dat) +
  theme_minimal() +
  geom_rect(aes(x = pct_change, y = athlete), xmin = -3, xmax = 3,
                ymin = as.numeric(dat$athlete[[13]]) - 0.6,
                ymax = as.numeric(dat$athlete[[18]]) + 0.6,
            fill = "#F5F5F5", alpha = 0.1) +
  geom_vline(xintercept = c(-3, 0, 3), linetype = "dashed", size = 0.2) +
  geom_link(aes(x = 0, xend = pct_change, y = athlete, yend = athlete,
                colour = colour, alpha = stat(index)),
            show.legend = FALSE, size = 5, n = 600) +
  scale_colour_identity() +
  scale_x_continuous(limits = c(-8, 10),
                     breaks = scales::pretty_breaks(n = 11)) +
  labs(x = "Percentage Change in Jump Height (%)") +
  theme(panel.grid.minor.x = element_blank(),
        panel.grid.major.y = element_blank(),
        axis.title.x = element_text(face = "bold"),
        axis.title.y = element_blank())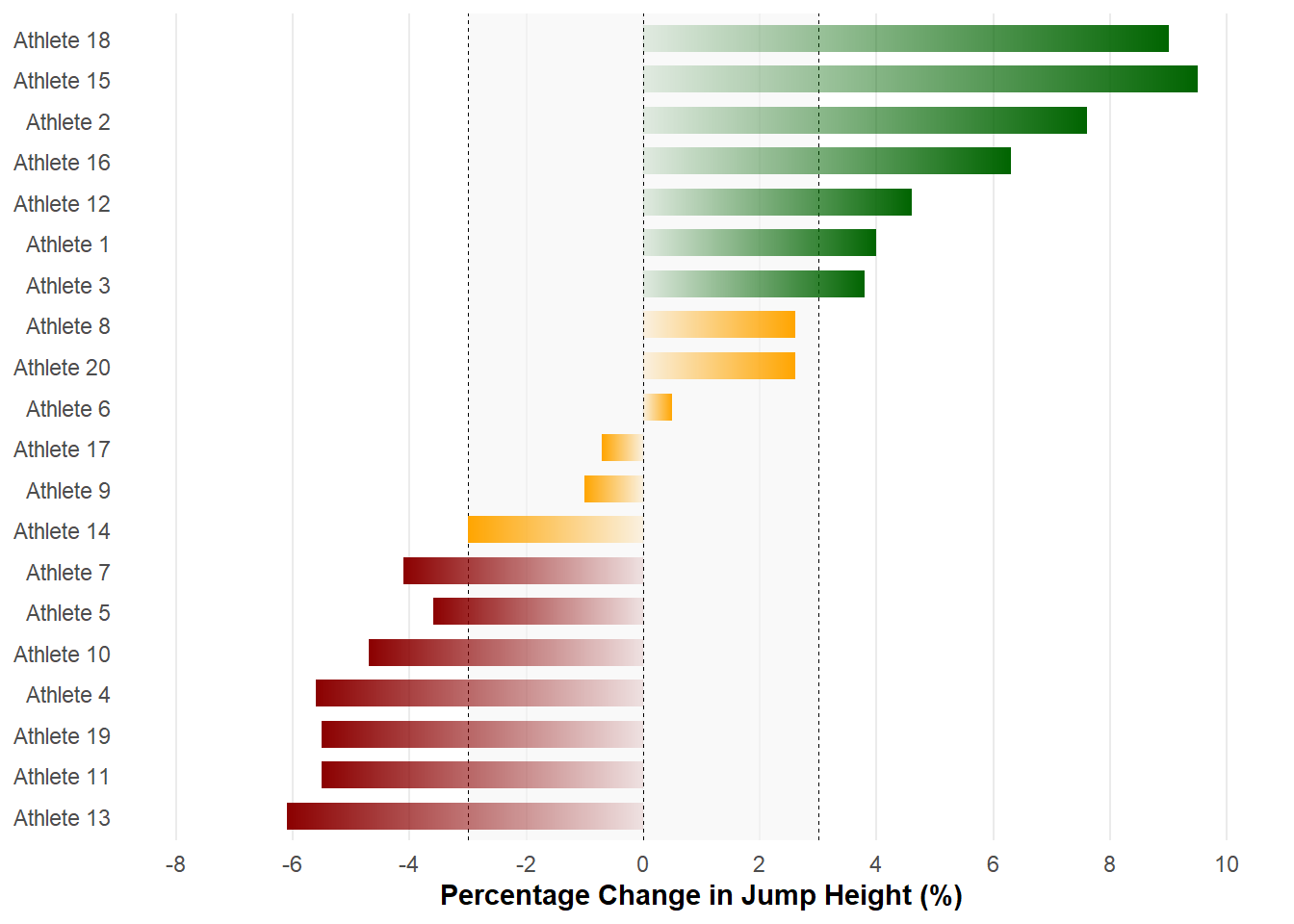

Again, I’m preferring the sequential colours with geom_link() over a traditional horizontal bar plot using geom_col(). We can compare visually our change scores relative to the cv as represented by the shaded area (geom_rect()) and vertical lines (geom_vline()).

Example 3

It may also be useful to plot the swc to visualise the threshold value that represents the smallest important effect when monitoring changes in performance tests. We can use the same approach as the example above by designating the boundaries of the swc with geom_rect() to visualise this threshold and plot points with their respective “uncertainty” (te) using geom_linerange().

ggplot(dat) +
  theme_minimal() +
  geom_rect(aes(x = change, y = athlete), xmin = -0.5, xmax = 0.5,
            ymin = as.numeric(dat$athlete[[13]]) - 0.6,
            ymax = as.numeric(dat$athlete[[18]]) + 0.6,
            fill = "#F5F5F5", alpha = 0.2) +
  geom_vline(xintercept = c(-0.5, 0, 0.5), linetype = "dashed", size = 0.2) +
  geom_linerange(aes(xmin = change - te, xmax = change + te, y = athlete,
                     colour = colour), size = 1.5, alpha = 0.8) +
  scale_colour_identity() +
  geom_point(aes(x = change, y = athlete, fill = colour), shape = 21,
             size = 4) +
  scale_fill_identity() +
  scale_x_continuous(breaks = scales::pretty_breaks(n = 9)) +
  labs(x = "Change in Jump Height (cm)") +
  theme(panel.grid.minor.x = element_blank(),
        panel.grid.major.y = element_blank(),
        axis.title.x = element_text(face = "bold"),
        axis.title.y = element_blank())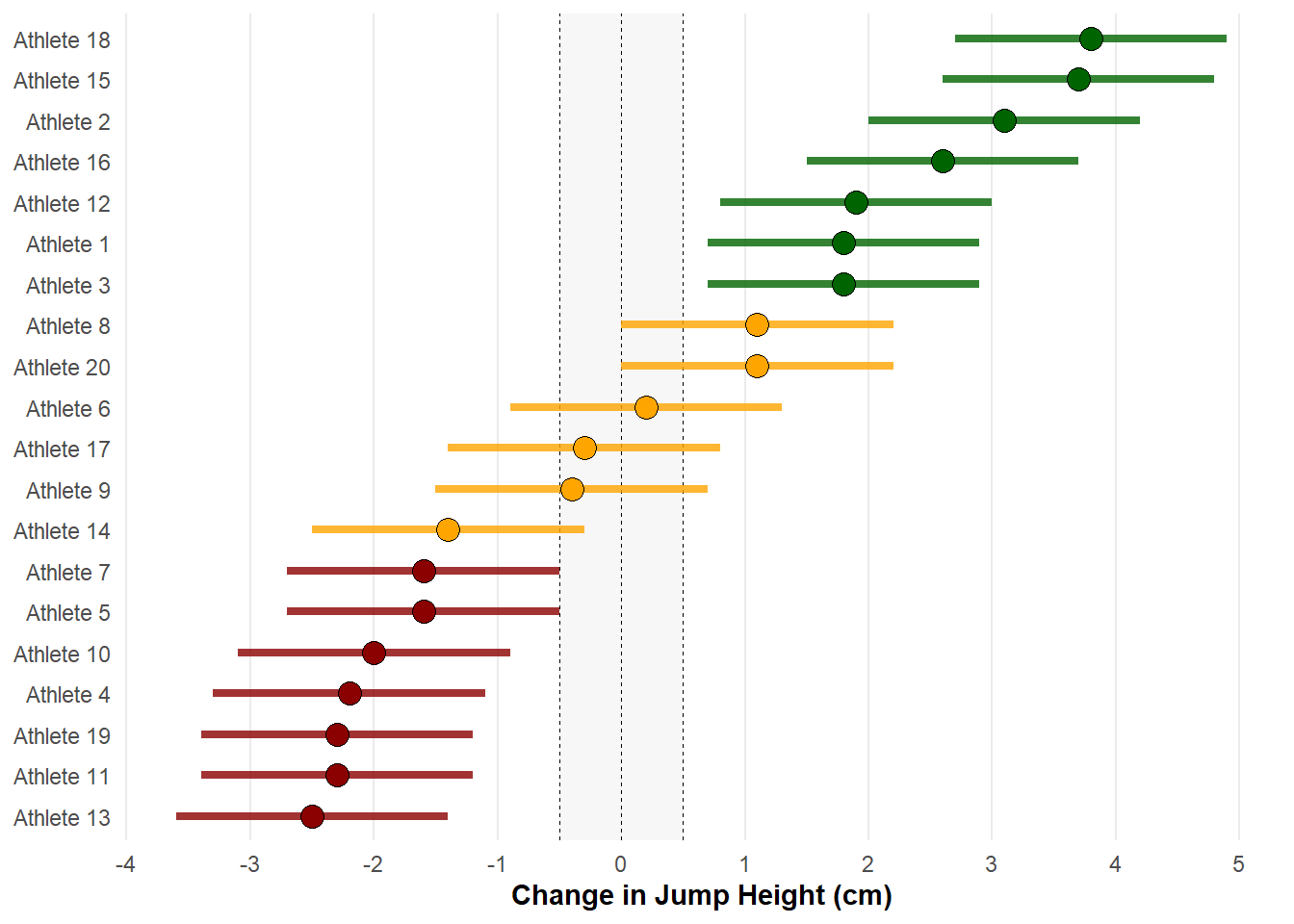

We can set the uncertainty for each athlete’s test result by subtracting and adding the te to the raw change score in the xmin = and xmax = arguments, respectively. As you’ll see, those data points crossing the swc are coloured orange to denote a trivial or unclear change in jump height.

Hopefully, these examples have given you some ideas as to how you may visualise change scores for your athletes and lean on fundamental reliability concepts to inform your interpretation. There are many ways to customise these plotting examples further beyond what I’ve highlighted here, so be sure to give these a try using your own data.